［本站讯］近日，国际流体力学顶级期刊Journal of Fluid Mechanics(简称JFM)发表了数学学院芮洪兴教授课题组的研究成果Superconvergence of a fully conservative finite difference method on non-uniform staggered grids for simulating wormhole propagation with the Darcy_Brinkman_Forchheimer framework (JFM, Vol. 872(2019): 438-471)。芮洪兴教授为该论文唯一通讯作者, 学院博士毕业生李晓丽为第一作者。

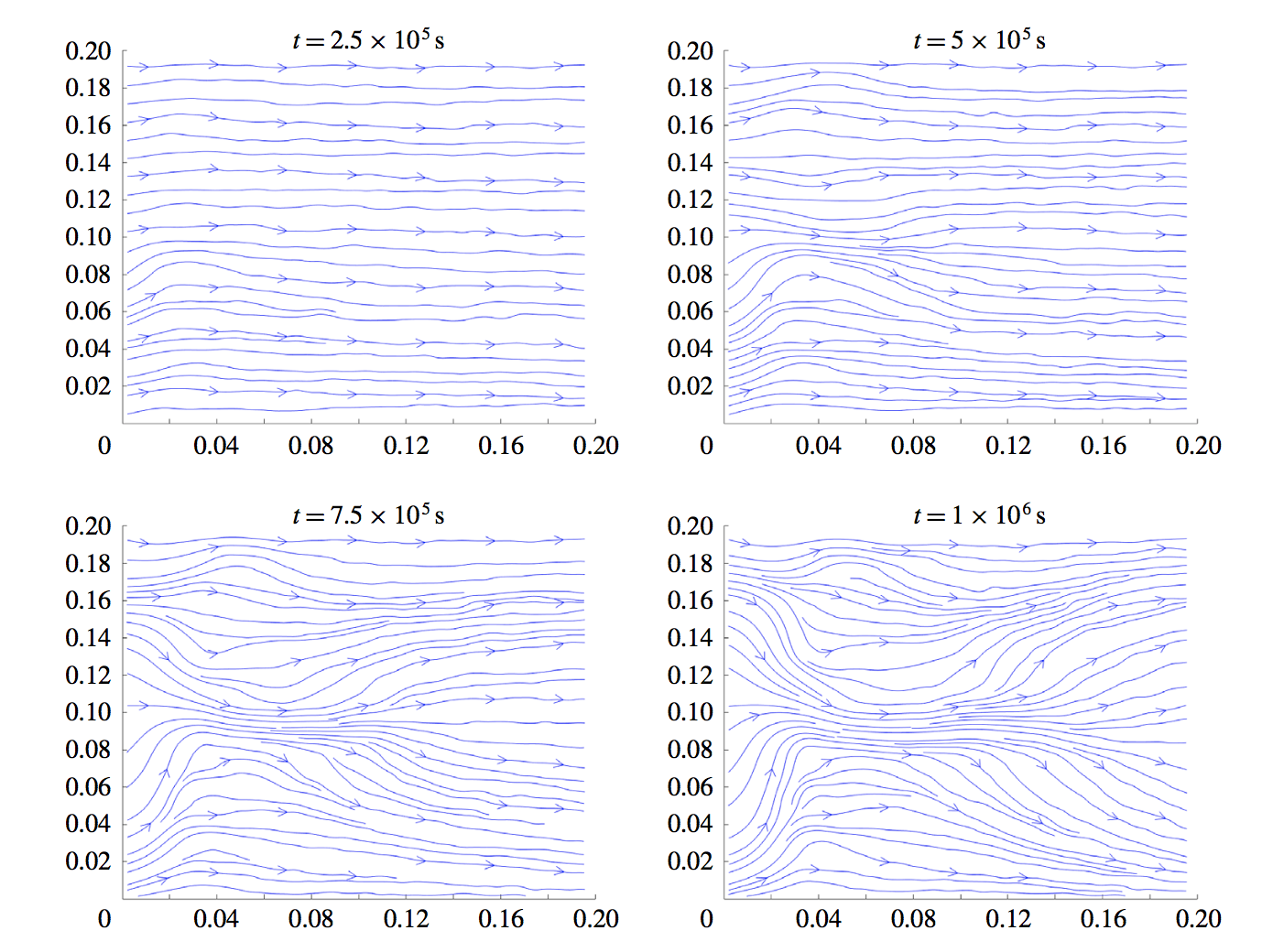
酸蚀蚓孔模型广泛应用于石油、天然气、二氧化碳等地下流体资源开发。蚓孔的形成须经一系列复杂的物理化学反应，其中储层孔隙度、酸的浓度、储层压力等都会对碳酸盐岩储层酸化过程有直接的影响，刻画蚓孔变化形态的非线性数学模型非常复杂，不可能得到解析解。因此数值求解变得尤为重要。为此，芮洪兴教授团队针对Darcy-Brinkman -Forchheimer框架下的酸蚀蚓孔模型，考虑从混合元、间断元、有限体积等不同的方法出发构造全解耦守恒型交错网格有限差分算法，研究得到其在非一致网格上的超收敛性。进行数值实验模拟孔隙度和酸的浓度的演变过程，展示碳酸盐岩储层的酸化过程，数值结果对油气采集具有指导作用。

JFM由剑桥大学创办，被公认为流体力学领域最著名的顶级期刊，在流体力学领域国际排名第一。据悉，该论文是山东大学首次作为通讯作者在该期刊发表研究成果。

论文链接：https://doi.org/10.1017/jfm.2019.399